Consider Clock Arithmetic Using a Clock with Four Numbers: 0

Essay

Consider clock arithmetic using a clock with four numbers: 0, 1, 2, and 3.
A) Complete these tables 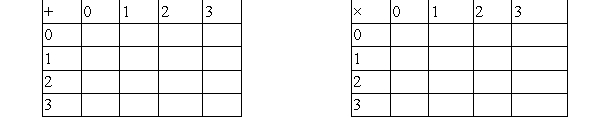B) Do you think the set of numbers-0, 1, 2, and 3-is closed under addition? If not, provide an example that shows it is not.
C) Do you think the set of numbers-0, 1, 2, and 3-is closed under multiplication? If not, provide an example that shows it is not.
D) Is there an additive identity? If so, what is it?
E) Is there a multiplicative identity? If so, what is it?
F) Does 3 have an additive inverse? If so, what is it?
G) Does 2 have a multiplicative inverse? If so, what is it?
H) Do you think addition is commutative? If so, how do we know that as we look at the table?
I) Do you think multiplication is commutative? If so, how do we know that as we look at the table?
J) Do you think addition is associative? If so, provide at least three examples.
K) Do you think multiplication is associative? If so, provide at least three examples.
L) Do you think multiplication is distributive over addition? If so, provide at least three examples.