Scenario: Alex Puts $100 on the Table

Multiple Choice

Scenario: Alex puts $100 on the table. Bob chooses either to take $51 for himself and $49 for Clare or pass. If Bob passes, then Alex adds another $2 and Clare chooses either to take $52 for herself and $50 for Bob or pass. If Clare passes, then Alex adds another $2 and Bob chooses either to take $53 for himself and $51 for Clare or pass, and so on. In other words, a player chooses either to take $2 more for himself/herself or pass, and, every time a player passes, Alex adds another $2. The game ends if $200 is on the table or either Bob or Clare chooses not to pass before that. If the amount on the table reached $200, then Bob and Clare get $99.99 each (Alex takes two pennies back) . The figure below shows the extensive form of this game. Bob's payoff is written first and Clare's second.

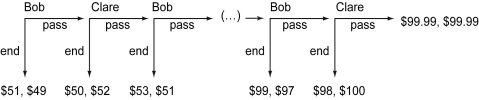
-Refer to the scenario above.If the game reached Clare's turn with $198 on the table,she should ________.

A) end the game
B) either pass or end the game
C) pass
D) neither pass nor end the game