Solved

Identify the Conic Section as a Parabola, Ellipse, Circle, or Hyperbola:The

Question 166

Multiple Choice

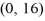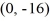Identify the conic section as a parabola, ellipse, circle, or hyperbola:The set of all points whose difference of the distances to the points Identify the conic section as a parabola, ellipse, circle, or hyperbola:The set of all points whose difference of the distances to the points and is exactly 18 units. A) parabola B) ellipse C) circle D) hyperbola and Identify the conic section as a parabola, ellipse, circle, or hyperbola:The set of all points whose difference of the distances to the points and is exactly 18 units. A) parabola B) ellipse C) circle D) hyperbola is exactly 18 units.


A) parabola
B) ellipse
C) circle
D) hyperbola

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q161: Find the general form of the equation

Q162: Find the focus of the parabola with

Q163: Graph the ellipse. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1040/.jpg" alt="Graph the

Q164: Match the graph to the nonlinear inequality.

Q165: Find the standard form of the equation

Q167: Write an equation for the parabola. <img

Q168: Solve the system of equations by applying

Q169: Find the standard form of the ellipse

Q170: Find the vertex of the parabola with

Q171: Find the standard form of the hyperbola