Solved

The Function F (X) = + 6, X

Question 159

Multiple Choice

The function f (x) = 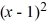The function f (x) = + 6, x ? 1 is a one-to-one function. Verify that + 5 is its inverse. A) The function is not the inverse of f (x) B) The function is the inverse of f (x) C) The function f (x) does not have an inverse + 6, x ? 1 is a one-to-one function. Verify that The function f (x) = + 6, x ? 1 is a one-to-one function. Verify that + 5 is its inverse. A) The function is not the inverse of f (x) B) The function is the inverse of f (x) C) The function f (x) does not have an inverse + 5 is its inverse.


A) The function is not the inverse of f (x)
B) The function is the inverse of f (x)
C) The function f (x) does not have an inverse

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q152: Graph the piecewise-defined function. State the domain

Q153: Given the functions f (x) = and

Q154: Determine if the equation x = <img

Q155: Given the function G(t) = <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1040/.jpg"

Q156: Given the functions <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1040/.jpg" alt="Given the

Q157: Write an equation that describes the variation.

Q158: The graph of y = <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1040/.jpg"

Q160: Determine if the function g(x) = 3

Q161: Write an equation that describes the variation.

Q162: Determine whether the function is a one-to-one