Solved

The Number of Standard Deviations Z That a Particular Value

Question 6

Multiple Choice

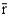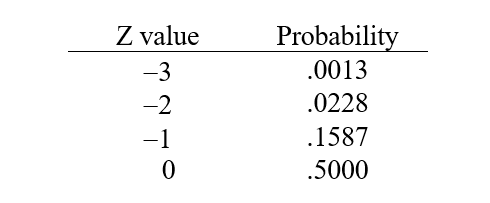
The number of standard deviations z that a particular value of r is from the mean The number of standard deviations z that a particular value of r is from the mean can be computed as .Suppose that you work as a commission-only insurance agent earning $1,000 per week on average. Suppose that your standard deviation of weekly earnings is $500. What is the probability that you zero in a week? Use the following brief z-table to help with this problem. A) 1.3% chance of earning nothing in a week B) 2.28% chance of earning nothing in a week C) 15.87% chance of earning nothing in a week D) 50% chance of earning nothing in a week E) none of the above can be computed as The number of standard deviations z that a particular value of r is from the mean can be computed as .Suppose that you work as a commission-only insurance agent earning $1,000 per week on average. Suppose that your standard deviation of weekly earnings is $500. What is the probability that you zero in a week? Use the following brief z-table to help with this problem. A) 1.3% chance of earning nothing in a week B) 2.28% chance of earning nothing in a week C) 15.87% chance of earning nothing in a week D) 50% chance of earning nothing in a week E) none of the above .Suppose that you work as a commission-only insurance agent earning $1,000 per week on average. Suppose that your standard deviation of weekly earnings is $500. What is the probability that you zero in a week? Use the following brief z-table to help with this problem. The number of standard deviations z that a particular value of r is from the mean can be computed as .Suppose that you work as a commission-only insurance agent earning $1,000 per week on average. Suppose that your standard deviation of weekly earnings is $500. What is the probability that you zero in a week? Use the following brief z-table to help with this problem. A) 1.3% chance of earning nothing in a week B) 2.28% chance of earning nothing in a week C) 15.87% chance of earning nothing in a week D) 50% chance of earning nothing in a week E) none of the above


A) 1.3% chance of earning nothing in a week
B) 2.28% chance of earning nothing in a week
C) 15.87% chance of earning nothing in a week
D) 50% chance of earning nothing in a week
E) none of the above

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q1: A Real Option Value is:<br>A) An option

Q2: Which of the following will increase

Q3: Complete the following table. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9871/.jpg" alt="Complete

Q4: A firm has decided to invest in

Q5: An investment advisor plans a portfolio

Q7: What are the expected net profits to

Q8: Recently, the American Medical Association changed its

Q9: Consider an investment with the following payoffs