Multiple Choice
Suppose a population has the characteristics listed below.
(a) A total of 60% of the population survives its first year. Of that 60%, 50% survives the second year. The maximum life span is 3 years.
(b) The average number of offspring for each member of the population is 4 the first year, 5 the second year, and 4 the third year.The population now consists of 150 members in each of the three age class. How many members will be in each age class after one year? After two years? Let  , and
, and  be vectors whose components are the number members in each age class after one year and after two years respectively.
be vectors whose components are the number members in each age class after one year and after two years respectively.
A) 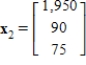 and
and 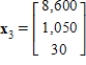
B)  and
and 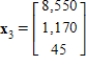
C) 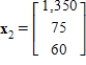 and
and 
D) 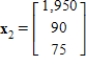 and
and 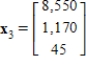
E) 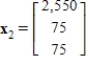 and
and 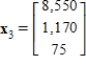
Correct Answer:

Verified
Correct Answer:
Verified
Q14: Use the age transition matrix <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9901/.jpg"
Q15: Find the eigenvalues and corresponding eigenvectors for
Q16: Find the eigenvalues and corresponding eigenvectors for
Q17: Find a stable age distribution for the
Q18: Which of the following is an eigenvector
Q20: The matrix <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9901/.jpg" alt=" The
Q21: Find a nonsingular matrix <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9901/.jpg" alt="Find
Q22: Use the Principal Axes Theorem to perform
Q23: Find the eigenvalues of the symmetric matrix
Q24: Find an orthogonal matrix P such that