Solved

Determine Whether Is a Basis for

Question 3

Multiple Choice

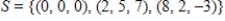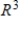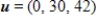Determine whether Determine whether is a basis for . If it is, write as a linear combination of the vectors in S.? A) S is a basis for and B) S is a basis for and ? C) S is a basis for and D) S is a basis for and E) S is not a basis for is a basis for Determine whether is a basis for . If it is, write as a linear combination of the vectors in S.? A) S is a basis for and B) S is a basis for and ? C) S is a basis for and D) S is a basis for and E) S is not a basis for . 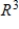If it is, write Determine whether is a basis for . If it is, write as a linear combination of the vectors in S.? A) S is a basis for and B) S is a basis for and ? C) S is a basis for and D) S is a basis for and E) S is not a basis for as a linear combination of the vectors in S.?


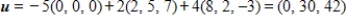
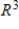A) S is a basis for Determine whether is a basis for . If it is, write as a linear combination of the vectors in S.? A) S is a basis for and B) S is a basis for and ? C) S is a basis for and D) S is a basis for and E) S is not a basis for and Determine whether is a basis for . If it is, write as a linear combination of the vectors in S.? A) S is a basis for and B) S is a basis for and ? C) S is a basis for and D) S is a basis for and E) S is not a basis for
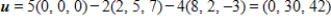
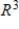B) S is a basis for Determine whether is a basis for . If it is, write as a linear combination of the vectors in S.? A) S is a basis for and B) S is a basis for and ? C) S is a basis for and D) S is a basis for and E) S is not a basis for and ? Determine whether is a basis for . If it is, write as a linear combination of the vectors in S.? A) S is a basis for and B) S is a basis for and ? C) S is a basis for and D) S is a basis for and E) S is not a basis for
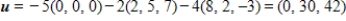
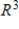C) S is a basis for Determine whether is a basis for . If it is, write as a linear combination of the vectors in S.? A) S is a basis for and B) S is a basis for and ? C) S is a basis for and D) S is a basis for and E) S is not a basis for and Determine whether is a basis for . If it is, write as a linear combination of the vectors in S.? A) S is a basis for and B) S is a basis for and ? C) S is a basis for and D) S is a basis for and E) S is not a basis for
D) S is a basis for Determine whether is a basis for . If it is, write as a linear combination of the vectors in S.? A) S is a basis for and B) S is a basis for and ? C) S is a basis for and D) S is a basis for and E) S is not a basis for and Determine whether is a basis for . If it is, write as a linear combination of the vectors in S.? A) S is a basis for and B) S is a basis for and ? C) S is a basis for and D) S is a basis for and E) S is not a basis for
E) S is not a basis for Determine whether is a basis for . If it is, write as a linear combination of the vectors in S.? A) S is a basis for and B) S is a basis for and ? C) S is a basis for and D) S is a basis for and 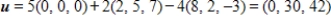E) S is not a basis for

Correct Answer:

verifed

Verified

Related Questions

Q1: Describe the zero vector (the additive identity)

Q2: Find a basis for the subspace of

Q4: Describe the zero vector (the additive identity)

Q5: Find the coordinate matrix of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9901/.jpg"

Q6: ? The set <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9901/.jpg" alt="? The

Q7: Find the coordinate matrix of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9901/.jpg"

Q8: Find a basis for the row space

Q9: Find a basis for and the dimension

Q10: Perform a rotation of axes to eliminate

Q11: Provided <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9901/.jpg" alt="Provided and