Solved

The Eigenvalues of the Matrix Are and

Question 25

Multiple Choice

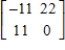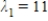The eigenvalues of the matrix The eigenvalues of the matrix are and . Find a non-zero eigenvector associated with each eigenvalue. A) , ; , B) , ; , C) , ; , D) , ; , E) , ; , are The eigenvalues of the matrix are and . Find a non-zero eigenvector associated with each eigenvalue. A) , ; , B) , ; , C) , ; , D) , ; , E) , ; , and The eigenvalues of the matrix are and . Find a non-zero eigenvector associated with each eigenvalue. A) , ; , B) , ; , C) , ; , D) , ; , E) , ; , . Find a non-zero eigenvector associated with each eigenvalue.


A) The eigenvalues of the matrix are and . Find a non-zero eigenvector associated with each eigenvalue. A) , ; , B) , ; , C) , ; , D) , ; , E) , ; , , The eigenvalues of the matrix are and . Find a non-zero eigenvector associated with each eigenvalue. A) , ; , B) , ; , C) , ; , D) , ; , E) , ; , ; The eigenvalues of the matrix are and . Find a non-zero eigenvector associated with each eigenvalue. A) , ; , B) , ; , C) , ; , D) , ; , E) , ; , , The eigenvalues of the matrix are and . Find a non-zero eigenvector associated with each eigenvalue. A) , ; , B) , ; , C) , ; , D) , ; , E) , ; ,
B) The eigenvalues of the matrix are and . Find a non-zero eigenvector associated with each eigenvalue. A) , ; , B) , ; , C) , ; , D) , ; , E) , ; , , The eigenvalues of the matrix are and . Find a non-zero eigenvector associated with each eigenvalue. A) , ; , B) , ; , C) , ; , D) , ; , E) , ; , ; The eigenvalues of the matrix are and . Find a non-zero eigenvector associated with each eigenvalue. A) , ; , B) , ; , C) , ; , D) , ; , E) , ; , , The eigenvalues of the matrix are and . Find a non-zero eigenvector associated with each eigenvalue. A) , ; , B) , ; , C) , ; , D) , ; , E) , ; ,
C) The eigenvalues of the matrix are and . Find a non-zero eigenvector associated with each eigenvalue. A) , ; , B) , ; , C) , ; , D) , ; , E) , ; , , The eigenvalues of the matrix are and . Find a non-zero eigenvector associated with each eigenvalue. A) , ; , B) , ; , C) , ; , D) , ; , E) , ; , ; The eigenvalues of the matrix are and . Find a non-zero eigenvector associated with each eigenvalue. A) , ; , B) , ; , C) , ; , D) , ; , E) , ; , , The eigenvalues of the matrix are and . Find a non-zero eigenvector associated with each eigenvalue. A) , ; , B) , ; , C) , ; , D) , ; , E) , ; ,
D) The eigenvalues of the matrix are and . Find a non-zero eigenvector associated with each eigenvalue. A) , ; , B) , ; , C) , ; , D) , ; , E) , ; , , The eigenvalues of the matrix are and . Find a non-zero eigenvector associated with each eigenvalue. A) , ; , B) , ; , C) , ; , D) , ; , E) , ; , ; The eigenvalues of the matrix are and . Find a non-zero eigenvector associated with each eigenvalue. A) , ; , B) , ; , C) , ; , D) , ; , E) , ; , , The eigenvalues of the matrix are and . Find a non-zero eigenvector associated with each eigenvalue. A) , ; , B) , ; , C) , ; , D) , ; , E) , ; ,
E) The eigenvalues of the matrix are and . Find a non-zero eigenvector associated with each eigenvalue. A) , ; , B) , ; , C) , ; , D) , ; , E) , ; , , The eigenvalues of the matrix are and . Find a non-zero eigenvector associated with each eigenvalue. A) , ; , B) , ; , C) , ; , D) , ; , E) , ; , ; The eigenvalues of the matrix are and . Find a non-zero eigenvector associated with each eigenvalue. A) , ; , B) , ; , C) , ; , D) , ; , E) , ; , , The eigenvalues of the matrix are and 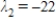. Find a non-zero eigenvector associated with each eigenvalue. 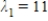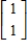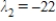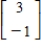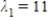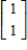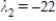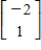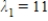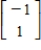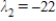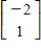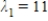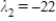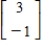A) , ; , B) , ; , C) , ; , D) , ; , E) , ; ,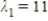

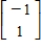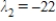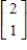
Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q20: Find the determinant of the elementary matrix

Q21: Let A and B be square matrices

Q22: Which property of determinants is illustrated by

Q23: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9901/.jpg" alt="Evaluate for

Q24: Find the determinant of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9901/.jpg" alt="Find

Q26: Use the determinant to decide whether the

Q27: Find the characteristic equation of the matrix

Q28: Use elementary row or column operations to

Q29: Find the eigenvalues of the matrix <img

Q30: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9901/.jpg" alt="Evaluate for