Solved

Find the Eigenvalues of the Matrix

Question 38

Multiple Choice

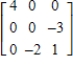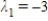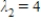Find the eigenvalues of the matrix Find the eigenvalues of the matrix . If an eigenvalue has multiplicity greater than one, list the eigenvalue according to its multiplicity. For example, list an eigenvalue with multiplicity two twice. A) , , and B) , , and C) , , and D) , , and E) , , and . If an eigenvalue has multiplicity greater than one, list the eigenvalue according to its multiplicity. For example, list an eigenvalue with multiplicity two twice.


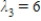
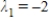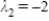A) Find the eigenvalues of the matrix . If an eigenvalue has multiplicity greater than one, list the eigenvalue according to its multiplicity. For example, list an eigenvalue with multiplicity two twice. A) , , and B) , , and C) , , and D) , , and E) , , and , Find the eigenvalues of the matrix . If an eigenvalue has multiplicity greater than one, list the eigenvalue according to its multiplicity. For example, list an eigenvalue with multiplicity two twice. 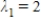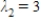A) , , and B) , , and C) , , and D) , , and E) , , and , and Find the eigenvalues of the matrix . If an eigenvalue has multiplicity greater than one, list the eigenvalue according to its multiplicity. For example, list an eigenvalue with multiplicity two twice. A) , , and B) , , and C) , , and D) , , and E) , , and
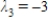
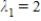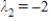B) Find the eigenvalues of the matrix . If an eigenvalue has multiplicity greater than one, list the eigenvalue according to its multiplicity. For example, list an eigenvalue with multiplicity two twice. A) , , and B) , , and C) , , and D) , , and E) , , and , Find the eigenvalues of the matrix . If an eigenvalue has multiplicity greater than one, list the eigenvalue according to its multiplicity. For example, list an eigenvalue with multiplicity two twice. 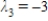A) , , and B) , , and C) , , and D) , , and E) , , and , and Find the eigenvalues of the matrix . If an eigenvalue has multiplicity greater than one, list the eigenvalue according to its multiplicity. For example, list an eigenvalue with multiplicity two twice. A) , , and B) , , and C) , , and D) , , and E) , , and
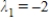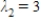C) Find the eigenvalues of the matrix . If an eigenvalue has multiplicity greater than one, list the eigenvalue according to its multiplicity. For example, list an eigenvalue with multiplicity two twice. A) , , and B) , , and C) , , and D) , , and E) , , and , Find the eigenvalues of the matrix . If an eigenvalue has multiplicity greater than one, list the eigenvalue according to its multiplicity. For example, list an eigenvalue with multiplicity two twice. A) , , and B) , , and C) , , and D) , , and E) , , and , and Find the eigenvalues of the matrix . If an eigenvalue has multiplicity greater than one, list the eigenvalue according to its multiplicity. For example, list an eigenvalue with multiplicity two twice. A) , , and B) , , and C) , , and D) , , and E) , , and
D) Find the eigenvalues of the matrix . If an eigenvalue has multiplicity greater than one, list the eigenvalue according to its multiplicity. For example, list an eigenvalue with multiplicity two twice. A) , , and B) , , and C) , , and D) , , and E) , , and , Find the eigenvalues of the matrix . If an eigenvalue has multiplicity greater than one, list the eigenvalue according to its multiplicity. For example, list an eigenvalue with multiplicity two twice. A) , , and B) , , and C) , , and D) , , and E) , , and , and Find the eigenvalues of the matrix . If an eigenvalue has multiplicity greater than one, list the eigenvalue according to its multiplicity. For example, list an eigenvalue with multiplicity two twice. A) , , and B) , , and C) , , and D) , , and E) , , and
E) Find the eigenvalues of the matrix . If an eigenvalue has multiplicity greater than one, list the eigenvalue according to its multiplicity. For example, list an eigenvalue with multiplicity two twice. A) , , and B) , , and C) , , and D) , , and E) , , and , Find the eigenvalues of the matrix . If an eigenvalue has multiplicity greater than one, list the eigenvalue according to its multiplicity. For example, list an eigenvalue with multiplicity two twice. A) , , and B) , , and C) , , and D) , , and E) , , and , and Find the eigenvalues of the matrix . If an eigenvalue has multiplicity greater than one, list the eigenvalue according to its multiplicity. For example, list an eigenvalue with multiplicity two twice. A) , , and B) , , and C) , , and D) , , and E) , , and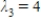

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q33: Find the eigenvalues of the matrix <img

Q34: Which property of determinants is illustrated by

Q35: Find the minor <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9901/.jpg" alt="Find the

Q36: Find the determinant of the elementary matrix

Q37: Find the characteristic equation of the matrix

Q39: Solve for x given the following equation

Q40: Determine whether the points <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9901/.jpg" alt="Determine

Q41: Evaluate the determinant. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9901/.jpg" alt="Evaluate the

Q42: Use the matrix capabilities of a graphing

Q43: Find the determinant of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9901/.jpg" alt="Find