Solved

Use the Method of Variation of Parameters to Find the General

Question 33

Essay

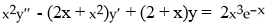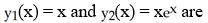Use the method of variation of parameters to find the general solution of the nonhomogeneous linear equation Use the method of variation of parameters to find the general solution of the nonhomogeneous linear equation given that are independent solutions of the corresponding homogeneous equation. given that Use the method of variation of parameters to find the general solution of the nonhomogeneous linear equation given that are independent solutions of the corresponding homogeneous equation. are independent solutions of the corresponding homogeneous equation.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q28: Solve the initial-value problem <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Solve

Q29: Let F(t) = <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Let F(t)

Q30: Use the improved Euler method to determine

Q31: State the order of the following differential

Q32: Find the general solution of the differential

Q34: Find all solutions to <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Find

Q35: Solve the initial-value problem <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Solve

Q36: Calculate the Laplace transform of F(t)

Q37: The nonexact differential equation M (t, x))

Q38: Use Euler's method to determine an approximate