The Fixed Point at the Origin of the Autonomous Linear

Multiple Choice

The fixed point at the origin of the autonomous linear system 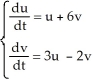is

A) a saddle point with the fixed point (0 , 0) being the omega limit for the trajectory v = - u and the alpha limit for the trajectory v = u.
B) a saddle point with the fixed point (0 , 0) being the omega limit for the trajectory v = u and the alpha limit for the trajectory v = - u.
C) a stable node with the fixed point at the origin being the limit point of all trajectories.
D) an unstable node with the fixed point at the origin being the limit point of all trajectories.
E) a saddle point with the fixed point (0 , 0) being the omega limit for the trajectory v = u and the alpha limit for the trajectory v = 2 u.