Solved

Consider the Autonomous Linear System Where a , B

Question 23

True/False

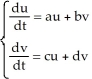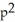Consider the autonomous linear system Consider the autonomous linear system where a , b , c, and d are constant real numbers. Let p = a + d, q = ad - bc, and r = - 4 q.If r > 0 and q < 0, then the fixed point at the origin is a saddle point. where a , b , c, and d are constant real numbers. Let p = a + d, q = ad - bc, and r = Consider the autonomous linear system where a , b , c, and d are constant real numbers. Let p = a + d, q = ad - bc, and r = - 4 q.If r > 0 and q < 0, then the fixed point at the origin is a saddle point. - 4 q.If r > 0 and q < 0, then the fixed point at the origin is a saddle point.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q18: Find a particular solution of the differential

Q19: Find F(t) ,the inverse Laplace transform of

Q20: Find the solution of the initial value

Q21: Solve the initial-value problem <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Solve

Q22: Transform the linear system <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Transform

Q24: Find all fixed points of the non-linear

Q25: Find the general solution of the differential

Q26: State the order of the following differential

Q27: Find the degree 3 Maclaurin polynomial for

Q28: Solve the initial-value problem <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Solve