Solved

Let the Differential 2-Form = (3

Question 42

Multiple Choice

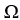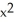Let the differential 2-form Let the differential 2-form = (3 + 2xy + 6 ) dx dy be defined in a star-like domain . (a) Is closed? (b) Is exact on D? If so, find a differential 1-form such that = d . 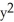A) is closed but not exact B) is both closed and exact, = - (x + 2 ) dx + dy C) is neither closed nor exact D) is both closed and exact, = (x + 2 ) dx + dy E) is both closed and exact, = dx - (x + 2 ) dy = (3 Let the differential 2-form = (3 + 2xy + 6 ) dx dy be defined in a star-like domain . (a) Is closed? (b) Is exact on D? If so, find a differential 1-form such that = d . 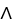A) is closed but not exact B) is both closed and exact, = - (x + 2 ) dx + dy C) is neither closed nor exact D) is both closed and exact, = (x + 2 ) dx + dy E) is both closed and exact, = dx - (x + 2 ) dy + 2xy + 6 Let the differential 2-form = (3 + 2xy + 6 ) dx dy be defined in a star-like domain . (a) Is closed? (b) Is exact on D? If so, find a differential 1-form such that = d . 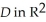A) is closed but not exact B) is both closed and exact, = - (x + 2 ) dx + dy C) is neither closed nor exact D) is both closed and exact, = (x + 2 ) dx + dy E) is both closed and exact, = dx - (x + 2 ) dy ) dxLet the differential 2-form = (3 + 2xy + 6 ) dx dy be defined in a star-like domain . (a) Is closed? (b) Is exact on D? If so, find a differential 1-form such that = d . A) is closed but not exact B) is both closed and exact, = - (x + 2 ) dx + dy C) is neither closed nor exact D) is both closed and exact, = (x + 2 ) dx + dy E) is both closed and exact, = dx - (x + 2 ) dy dy be defined in a star-like domain Let the differential 2-form = (3 + 2xy + 6 ) dx dy be defined in a star-like domain . (a) Is closed? (b) Is exact on D? If so, find a differential 1-form such that = d . A) is closed but not exact B) is both closed and exact, = - (x + 2 ) dx + dy C) is neither closed nor exact D) is both closed and exact, = (x + 2 ) dx + dy E) is both closed and exact, = dx - (x + 2 ) dy .
(a) Is 11ee7bc9_5715_4a9c_ae82_31f72d013c41_TB9661_11 closed?
(b) Is 11ee7bc9_5715_4a9c_ae82_31f72d013c41_TB9661_11 exact on D? If so, find a differential 1-form 11ee7bc9_84dc_f4fe_ae82_1b41b7d4ea2f_TB9661_11 such that 11ee7bc9_5715_4a9c_ae82_31f72d013c41_TB9661_11 = d11ee7bc9_84dc_f4fe_ae82_1b41b7d4ea2f_TB9661_11 .


A) 11ee7bc9_5715_4a9c_ae82_31f72d013c41_TB9661_11 is closed but not exact
B) 11ee7bc9_5715_4a9c_ae82_31f72d013c41_TB9661_11 is both closed and exact, 11ee7bc9_84dc_f4fe_ae82_1b41b7d4ea2f_TB9661_11 = - (x 11ee77e1_7790_822f_a0f8_cfcabba15689_TB9661_11 + 2 11ee77e1_7790_8230_a0f8_5faaf7819df3_TB9661_11 ) dx + 11ee77e1_7790_8231_a0f8_abc3d5eaae96_TB9661_11 dy
C) 11ee7bc9_5715_4a9c_ae82_31f72d013c41_TB9661_11 is neither closed nor exact
D) 11ee7bc9_5715_4a9c_ae82_31f72d013c41_TB9661_11 is both closed and exact, 11ee7bc9_84dc_f4fe_ae82_1b41b7d4ea2f_TB9661_11 = (x 11ee77e1_7790_8232_a0f8_55a6027c73fd_TB9661_11 + 2 11ee77e1_7790_8233_a0f8_0b4d11046402_TB9661_11 ) dx + 11ee77e1_7790_a944_a0f8_8f25cd10593b_TB9661_11 dy
E) 11ee7bc9_5715_4a9c_ae82_31f72d013c41_TB9661_11 is both closed and exact, 11ee7bc9_84dc_f4fe_ae82_1b41b7d4ea2f_TB9661_11 = 11ee77e1_7790_a945_a0f8_0708c0d434ad_TB9661_11 dx - (x 11ee77e1_7790_a946_a0f8_8f0c49d6bc1a_TB9661_11 + 2 11ee77e1_7790_a947_a0f8_3f7673b68c8f_TB9661_11 ) dy

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q37: Find all values of the real

Q38: Integrate the differential (n -1)-form

Q39: One way to describe a smooth k-manifold

Q40: Prove that every smooth exterior derivative is

Q41: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt=" Let

Q43: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Find d

Q44: Let M be the smooth 2-manifold

Q45: Which of the following is an antiderivative

Q46: Let F(x, y) and G(x, y) be

Q47: Find the dimension of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Find