Solved

If M Is the Part of the Surface Z =

Question 6

True/False

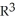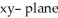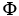If M is the part of the surface z = g(x, y) in If M is the part of the surface z = g(x, y) in that lies above a closed region D in the , then the integral of the differential 2-form = f(x, y) dx dy over M is independent of the function g. that lies above a closed region D in the If M is the part of the surface z = g(x, y) in that lies above a closed region D in the , then the integral of the differential 2-form = f(x, y) dx dy over M is independent of the function g. 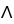, then the integral of the differential 2-form If M is the part of the surface z = g(x, y) in that lies above a closed region D in the , then the integral of the differential 2-form = f(x, y) dx dy over M is independent of the function g. = f(x, y) dxIf M is the part of the surface z = g(x, y) in that lies above a closed region D in the , then the integral of the differential 2-form = f(x, y) dx dy over M is independent of the function g. dy over M is independent of the function g.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q1: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt=" A)

Q2: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt=" = 0 for

Q3: Simplify a dx<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Simplify a dx

Q4: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Find d

Q5: Let [r, θ, z] be the cylindrical

Q7: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Let

Q8: Let k and n be integers such

Q9: Let D be a closed bounded domain

Q10: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt=" Let

Q11: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Let =