Multiple Choice
Find all values of the nonzero constant real numbers a, b, and c so that the vector field F = a cos( 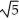 x + 2y ) cosh (c z) i + b cos (
x + 2y ) cosh (c z) i + b cos ( 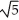 x + 2y) cosh (c z) j + c sin(
x + 2y) cosh (c z) j + c sin( 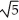 x + 2y) sinh(c z) k is both and .
x + 2y) sinh(c z) k is both and .
A) a = - 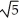 , b = -2, c = 3
, b = -2, c = 3
B) a = 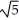 , b = 2, c = 2
, b = 2, c = 2
C) a = - 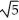 , b = -2, c =
, b = -2, c = 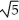 ± 2
± 2
D) a = 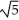 , b = 2, c = ± 3
, b = 2, c = ± 3
E) a = 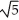 , b = -2, c = 9
, b = -2, c = 9
Correct Answer:

Verified
Correct Answer:
Verified
Q30: Use Stokes's Theorem to evaluate the line
Q31: Use Green's theorem in the plane to
Q32: A vector field F is called
Q33: In spherical coordinates, find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg"
Q34: If C is the positively oriented boundary
Q36: Using spherical polar coordinates, find <img
Q37: Evaluate the integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Evaluate the
Q38: Find the flux of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Find
Q39: Use Green's Theorem to compute the
Q40: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Evaluate clockwise