Solved

Let C Be a Non-Self-Intersecting Closed Curve in the Xy-Plane

Question 82

Multiple Choice

Let C be a non-self-intersecting closed curve in the xy-plane oriented counterclockwise and bounding a region R having area A and centroid Let C be a non-self-intersecting closed curve in the xy-plane oriented counterclockwise and bounding a region R having area A and centroid . In terms of these quantities, evaluate the line integral . A) A B) A C) A D) A E) -A . In terms of these quantities, evaluate the line integral Let C be a non-self-intersecting closed curve in the xy-plane oriented counterclockwise and bounding a region R having area A and centroid . In terms of these quantities, evaluate the line integral . A) A B) A C) A D) A E) -A .


A) A Let C be a non-self-intersecting closed curve in the xy-plane oriented counterclockwise and bounding a region R having area A and centroid . In terms of these quantities, evaluate the line integral . A) A B) A C) A D) A E) -A
B) A Let C be a non-self-intersecting closed curve in the xy-plane oriented counterclockwise and bounding a region R having area A and centroid . In terms of these quantities, evaluate the line integral . A) A B) A C) A D) A E) -A
C) A Let C be a non-self-intersecting closed curve in the xy-plane oriented counterclockwise and bounding a region R having area A and centroid . In terms of these quantities, evaluate the line integral . A) A B) A C) A D) A E) -A
D) A Let C be a non-self-intersecting closed curve in the xy-plane oriented counterclockwise and bounding a region R having area A and centroid . In terms of these quantities, evaluate the line integral . A) A B) A C) A D) A E) -A
E) -A Let C be a non-self-intersecting closed curve in the xy-plane oriented counterclockwise and bounding a region R having area A and centroid 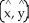. In terms of these quantities, evaluate the line integral 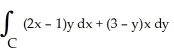. A) A 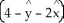B) A 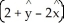C) A 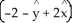D) A 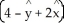E) -A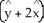

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q77: Evaluate the line integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg"

Q78: Use the Divergence Theorem to find

Q79: Let F = (z - y)

Q80: Use Green's Theorem to compute the integral

Q81: For r = x i + y

Q83: Find the flux of F = x

Q84: Using spherical polar coordinates, find <img

Q85: Given F = 4y i +

Q86: If r = x i + y

Q87: Evaluate the surface integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Evaluate