Multiple Choice
Evaluate 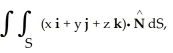 where S is the first-octant part of the sphere of radius a centred at the origin. (Hint: Even though S is not a closed surface, it is still easiest to use the Divergence Theorem because the integrand in the surface integral is zero on the coordinate planes.)
where S is the first-octant part of the sphere of radius a centred at the origin. (Hint: Even though S is not a closed surface, it is still easiest to use the Divergence Theorem because the integrand in the surface integral is zero on the coordinate planes.)
A) 
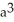
B) 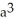
C) 

D) 2 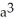
E) 
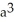
Correct Answer:

Verified
Correct Answer:
Verified
Q18: Use a line integral to find
Q19: Use Stokes's Theorem to evaluate the line
Q20: Verify that the vector field F =
Q21: Define the curl of a vector field
Q22: If r = x i + y
Q24: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Let and F
Q25: Let F = - <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg"
Q26: In cylindrical coordinates, find<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="
Q27: In cylindrical coordinates, find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg"
Q28: Use Stokes's Theorem to evaluate the