Multiple Choice
The local bases in cylindrical coordinates (r , , z) are given by  = cos( ) i + sin( ) j ,
= cos( ) i + sin( ) j , 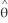 = - sin( ) i + cos( ) j, and
= - sin( ) i + cos( ) j, and  = k.
= k.
Express the acceleration a of a moving particle in space in terms of the local bases above.
A) 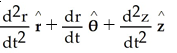
B) 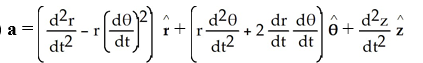
C) 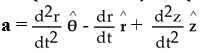
D) 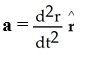
E) 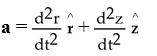
Correct Answer:

Verified
Correct Answer:
Verified
Q57: The divergence of a vector field F
Q58: Compute the divergence for the vector field
Q59: Show that there does not exist
Q60: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt=" Let
Q61: Evaluate the integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="
Q63: If <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="If ×
Q64: Evaluate the integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Evaluate the
Q65: A certain region R in 3-space has
Q66: Use Green's Theorem to compute <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg"
Q67: Compute <span class="ql-formula" data-value="\textbf{