Solved

Evaluate Where E Is the Region Enclosed by the Ellipsoid

Question 21

Multiple Choice

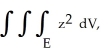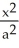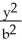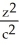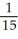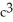
Evaluate Evaluate where E is the region enclosed by the ellipsoid + + = 1, a, b, c > 0. Use the transformation x = au, y = bv, z = cw. A) ab B) ab C) ab D) ab E) ab where E is the region enclosed by the ellipsoid Evaluate where E is the region enclosed by the ellipsoid + + = 1, a, b, c > 0. Use the transformation x = au, y = bv, z = cw. A) ab B) ab C) ab D) ab E) ab +Evaluate where E is the region enclosed by the ellipsoid + + = 1, a, b, c > 0. Use the transformation x = au, y = bv, z = cw. 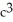A) ab B) ab C) ab D) ab E) ab + Evaluate where E is the region enclosed by the ellipsoid + + = 1, a, b, c > 0. Use the transformation x = au, y = bv, z = cw. A) ab B) ab C) ab D) ab E) ab = 1, a, b, c > 0. Use the transformation x = au, y = bv, z = cw.


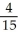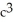
A) Evaluate where E is the region enclosed by the ellipsoid + + = 1, a, b, c > 0. Use the transformation x = au, y = bv, z = cw. A) ab B) ab C) ab D) ab E) ab ab Evaluate where E is the region enclosed by the ellipsoid + + = 1, a, b, c > 0. Use the transformation x = au, y = bv, z = cw. A) ab B) ab C) ab D) ab E) ab
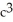
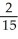B) Evaluate where E is the region enclosed by the ellipsoid + + = 1, a, b, c > 0. Use the transformation x = au, y = bv, z = cw. A) ab B) ab C) ab D) ab E) ab ab Evaluate where E is the region enclosed by the ellipsoid + + = 1, a, b, c > 0. Use the transformation x = au, y = bv, z = cw. A) ab B) ab C) ab D) ab E) ab
C) Evaluate where E is the region enclosed by the ellipsoid + + = 1, a, b, c > 0. Use the transformation x = au, y = bv, z = cw. A) ab B) ab C) ab D) ab E) ab ab Evaluate where E is the region enclosed by the ellipsoid + + = 1, a, b, c > 0. Use the transformation x = au, y = bv, z = cw. A) ab B) ab C) ab D) ab E) ab
D) Evaluate where E is the region enclosed by the ellipsoid + + = 1, a, b, c > 0. Use the transformation x = au, y = bv, z = cw. A) ab B) ab C) ab D) ab E) ab ab Evaluate where E is the region enclosed by the ellipsoid + + = 1, a, b, c > 0. Use the transformation x = au, y = bv, z = cw. A) ab B) ab C) ab D) ab E) ab
E) Evaluate where E is the region enclosed by the ellipsoid + + = 1, a, b, c > 0. Use the transformation x = au, y = bv, z = cw. A) ab B) ab C) ab D) ab E) ab ab Evaluate where E is the region enclosed by the ellipsoid + + = 1, a, b, c > 0. Use the transformation x = au, y = bv, z = cw. A) ab B) ab C) ab D) ab E) ab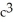

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q16: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt=" Evaluate

Q17: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt=" Evaluate

Q18: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Find where

Q19: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Evaluate dA,

Q20: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt=" Find

Q22: Evaluate the triple integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Evaluate

Q23: Find the surface area S of

Q24: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt=" Evaluate

Q25: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt=" Evaluate

Q26: Let E be the region in three-space