Multiple Choice
Find the absolute maximum and minimum values of f(x, y) = 4(x - x2) sin( y) on the rectangle 0 x 1, 0 y 2 and the points where they are assumed.
A) maximum 1 at  , minimum 0 at
, minimum 0 at 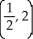
B) maximum 2 at 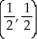 , minimum -2 at
, minimum -2 at 
C) maximum 1 at 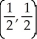 , minimum -1 at
, minimum -1 at 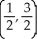
D) maximum 1 at 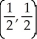 , minimum 0 at (0, 0) , (1, 0) , (0, 2) , and (1, 2)
, minimum 0 at (0, 0) , (1, 0) , (0, 2) , and (1, 2)
E) maximum 1 at 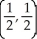 , minimum 0 at
, minimum 0 at 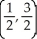
Correct Answer:

Verified
Correct Answer:
Verified
Q16: Find the absolute maximum and minimum
Q17: Starfleet Command has given Captain Kirk a
Q18: Use the fact that <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Use
Q19: Find the critical points of f(x, y)
Q20: Given F(<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Given F( )
Q22: Use Lagrange multipliers to find the maximum
Q23: Find the maximum and minimum distances from
Q24: The extreme values of the function f(x
Q25: Let pi > 0, i =
Q26: Find the point on the surface z