Solved

Find the Points Closest to the Origin on the Hyperbola

Question 11

Multiple Choice

Find the points closest to the origin on the hyperbola in which the cone x2 + y2 = z2 intersects the plane x + y = 2.


A) (1, 1, ± Find the points closest to the origin on the hyperbola in which the cone x<sup>2</sup> + y<sup>2</sup> = z<sup>2</sup> intersects the plane x + y = 2. A) (1, 1, ± ) B) (-1, -1, ± ) C) (-1, -1, ± ) and (1, 1, ± ) D) (2, 0, 2) and (0, 2, 2) E) (1, 1, ) and (-1, -1, - ) )
B) (-1, -1, ± Find the points closest to the origin on the hyperbola in which the cone x<sup>2</sup> + y<sup>2</sup> = z<sup>2</sup> intersects the plane x + y = 2. A) (1, 1, ± ) B) (-1, -1, ± ) C) (-1, -1, ± ) and (1, 1, ± ) D) (2, 0, 2) and (0, 2, 2) E) (1, 1, ) and (-1, -1, - ) )
C) (-1, -1, ± Find the points closest to the origin on the hyperbola in which the cone x<sup>2</sup> + y<sup>2</sup> = z<sup>2</sup> intersects the plane x + y = 2. A) (1, 1, ± ) B) (-1, -1, ± ) C) (-1, -1, ± ) and (1, 1, ± ) D) (2, 0, 2) and (0, 2, 2) E) (1, 1, ) and (-1, -1, - ) ) and (1, 1, ± Find the points closest to the origin on the hyperbola in which the cone x<sup>2</sup> + y<sup>2</sup> = z<sup>2</sup> intersects the plane x + y = 2. A) (1, 1, ± ) B) (-1, -1, ± ) C) (-1, -1, ± ) and (1, 1, ± ) D) (2, 0, 2) and (0, 2, 2) E) (1, 1, ) and (-1, -1, - ) )
D) (2, 0, 2) and (0, 2, 2)
E) (1, 1, Find the points closest to the origin on the hyperbola in which the cone x<sup>2</sup> + y<sup>2</sup> = z<sup>2</sup> intersects the plane x + y = 2. A) (1, 1, ± ) B) (-1, -1, ± ) C) (-1, -1, ± ) and (1, 1, ± ) D) (2, 0, 2) and (0, 2, 2) E) (1, 1, ) and (-1, -1, - ) ) and (-1, -1, - Find the points closest to the origin on the hyperbola in which the cone x<sup>2</sup> + y<sup>2</sup> = z<sup>2</sup> intersects the plane x + y = 2. A) (1, 1, ± 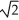) B) (-1, -1, ± 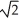) C) (-1, -1, ± 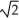) and (1, 1, ± 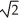) D) (2, 0, 2) and (0, 2, 2) E) (1, 1, 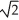) and (-1, -1, - ) )

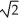Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q6: Find the maximum and minimum values of

Q7: Evaluate F(x,y) = <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Evaluate F(x,y)

Q8: Find and classify the critical points of

Q9: A rectangular box with no top has

Q10: Every one-parameter family of curves in the

Q12: Find and classify all critical points for

Q13: Find and classify the critical points

Q14: Suppose the critical points of f(x,y) =

Q15: Use Maple's fsolve with Digits : =

Q16: Find the absolute maximum and minimum