Solved

Find the Linearization L(x,y) of F(x,y) = X (Y)

Question 25

Multiple Choice

Find the linearization L(x,y) of f(x,y) = x Find the linearization L(x,y) of f(x,y) = x (y) about the point . A) B) C) D) E) (y) about the point Find the linearization L(x,y) of f(x,y) = x (y) about the point . A) B) C) D) E) .


A) Find the linearization L(x,y) of f(x,y) = x (y) about the point . A) B) C) D) E)
B) Find the linearization L(x,y) of f(x,y) = x (y) about the point . A) B) C) D) E)
C) Find the linearization L(x,y) of f(x,y) = x (y) about the point . A) B) C) D) E)
D) Find the linearization L(x,y) of f(x,y) = x (y) about the point . A) B) C) D) E)
E) Find the linearization L(x,y) of f(x,y) = x (y) about the point 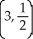. A) 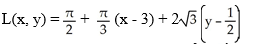B) 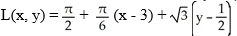C) 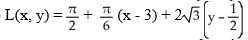D) 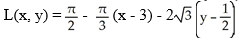E)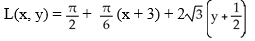

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q20: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt=" A)

Q21: Find the equation of the tangent plane

Q22: Find the differential of the function f(x,

Q23: Assuming that the function f has continuous

Q24: The linearization of f(x,y) =ln (x<sup>2</sup> +

Q26: Use the Jacobian matrix for the transformation

Q27: Suppose the system of equations <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg"

Q28: Find equations of the tangent line at

Q29: If the equations x = u<sup>2</sup> -

Q30: Find the Taylor series of the function