Solved

Find the Jacobian Matrix Df(x, Y, Z) of the Transformation

Question 38

Multiple Choice

Find the Jacobian matrix Df(x, y, z) of the transformation f(x, y, z) = (x2 + xy, y2 - ln(z) ) .


A) Find the Jacobian matrix Df(x, y, z) of the transformation f(x, y, z) = (x<sup>2</sup> + xy, y<sup>2</sup> - ln(z) ) . A) B) C) D) E)
B) Find the Jacobian matrix Df(x, y, z) of the transformation f(x, y, z) = (x<sup>2</sup> + xy, y<sup>2</sup> - ln(z) ) . A) B) C) D) E)
C) Find the Jacobian matrix Df(x, y, z) of the transformation f(x, y, z) = (x<sup>2</sup> + xy, y<sup>2</sup> - ln(z) ) . A) B) C) D) E)
D) Find the Jacobian matrix Df(x, y, z) of the transformation f(x, y, z) = (x<sup>2</sup> + xy, y<sup>2</sup> - ln(z) ) . A) B) C) D) E)
E) Find the Jacobian matrix Df(x, y, z) of the transformation f(x, y, z) = (x<sup>2</sup> + xy, y<sup>2</sup> - ln(z) ) . A) 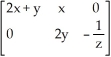B) 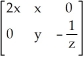C) 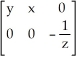D) 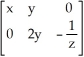E)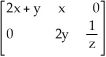

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q33: Evaluate the limit . <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg"

Q34: Find a unit vector in the

Q35: Find the distance from the point (0,

Q36: Find the directional derivative of f(x, y)

Q37: Find the value of the positive constant

Q39: Find the Taylor polynomial of degree 2

Q40: Describe the graph of the function f(x,y)

Q41: Evaluate the limit. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="

Q42: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Find and

Q43: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Find if