Solved

Given That the Relation Y2 + Y = 14

Question 56

Multiple Choice

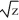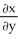Given that the relation y2 + y Given that the relation y<sup>2</sup> + y = 14 - sin(xz<sup>2</sup>) + implicitly defines x as a differentiable function of y and z, find at the point (0, 3, 4) . A) - B) 2 C) -8 D) - E) 8 = 14 - sin(xz2) + Given that the relation y<sup>2</sup> + y = 14 - sin(xz<sup>2</sup>) + implicitly defines x as a differentiable function of y and z, find at the point (0, 3, 4) . A) - B) 2 C) -8 D) - E) 8 implicitly defines x as a differentiable function of y and z, find Given that the relation y<sup>2</sup> + y = 14 - sin(xz<sup>2</sup>) + implicitly defines x as a differentiable function of y and z, find at the point (0, 3, 4) . A) - B) 2 C) -8 D) - E) 8 at the point (0, 3, 4) .


A) - Given that the relation y<sup>2</sup> + y = 14 - sin(xz<sup>2</sup>) + implicitly defines x as a differentiable function of y and z, find at the point (0, 3, 4) . A) - B) 2 C) -8 D) - E) 8
B) 2
C) -8
D) - Given that the relation y<sup>2</sup> + y = 14 - sin(xz<sup>2</sup>) + implicitly defines x as a differentiable function of y and z, find at the point (0, 3, 4) . A) - B) 2 C) -8 D) - E) 8
E) 8

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q51: Find an equation of the plane tangent

Q52: Given z = f(x, y) = <img

Q53: Assuming that the function f has continuous

Q54: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt=" A)

Q55: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Evaluate (3,

Q57: Show that the function g(x,y) = <img

Q58: Describe the level curves f(x, y) =

Q59: Find the slope of the tangent line

Q60: Find an equation of the plane tangent

Q61: Write the equation for the surface obtained