Solved

Find the Velocity, Speed, and Acceleration at Time T of a Particle

Question 3

Multiple Choice

Find the velocity, speed, and acceleration at time t of a particle that has position function r(t) = (2sin t) i + 6t j + (2cos t) k.


A) Find the velocity, speed, and acceleration at time t of a particle that has position function r(t) = (2sin t) i + 6t j + (2cos t) k. A) B) C) D) E)
B) Find the velocity, speed, and acceleration at time t of a particle that has position function r(t) = (2sin t) i + 6t j + (2cos t) k. A) B) C) D) E)
C) Find the velocity, speed, and acceleration at time t of a particle that has position function r(t) = (2sin t) i + 6t j + (2cos t) k. A) B) C) D) E)
D) Find the velocity, speed, and acceleration at time t of a particle that has position function r(t) = (2sin t) i + 6t j + (2cos t) k. A) B) C) D) E)
E) Find the velocity, speed, and acceleration at time t of a particle that has position function r(t) = (2sin t) i + 6t j + (2cos t) k. A) 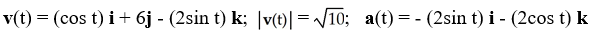B) 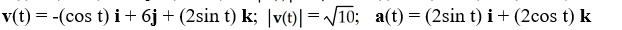C) D) 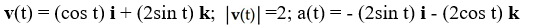E)

Correct Answer:

verifed

Verified

Related Questions

Q1: Reparametrize the curve r = <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg"

Q2: Suppose that the position r(t) and velocity

Q4: The mean distance from the Earth to

Q5: Find the length of the arc

Q6: Let C be the space curve given

Q7: Let r(t) = 4t i + 3sin(t)

Q8: The curve r = r(s) is a

Q9: A moving particle starts at an initial

Q10: The angular velocity of a certain comet

Q11: Solve the initial-value problem <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Solve