Solved

Solve the Initial-Value Problem = K × R with Initial

Question 60

Multiple Choice

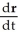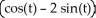Solve the initial-value problem Solve the initial-value problem = k × r with initial condition r(0) = i + 2j + 3k. Describe the solution curve. A) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. B) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. C) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. D) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. E) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. = k × r with initial condition r(0) = i + 2j + 3k. Describe the solution curve.


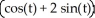A) r(t) = Solve the initial-value problem = k × r with initial condition r(0) = i + 2j + 3k. Describe the solution curve. A) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. B) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. C) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. D) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. E) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. 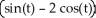i + Solve the initial-value problem = k × r with initial condition r(0) = i + 2j + 3k. Describe the solution curve. A) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. B) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. C) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. D) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. E) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3.
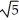B) r(t) = Solve the initial-value problem = k × r with initial condition r(0) = i + 2j + 3k. Describe the solution curve. A) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. B) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. C) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. D) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. E) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. 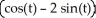i - Solve the initial-value problem = k × r with initial condition r(0) = i + 2j + 3k. Describe the solution curve. A) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. B) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. C) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. D) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. E) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. 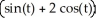j + 3 k,a circle with centre (0, 0, 3) and radius Solve the initial-value problem = k × r with initial condition r(0) = i + 2j + 3k. Describe the solution curve. A) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. B) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. C) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. D) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. E) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. in the plane z = 3.
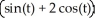C) r(t) = Solve the initial-value problem = k × r with initial condition r(0) = i + 2j + 3k. Describe the solution curve. A) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. B) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. C) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. D) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. E) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. 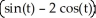i - Solve the initial-value problem = k × r with initial condition r(0) = i + 2j + 3k. Describe the solution curve. A) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. B) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. C) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. D) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. E) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3.
D) r(t) = Solve the initial-value problem = k × r with initial condition r(0) = i + 2j + 3k. Describe the solution curve. A) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. B) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. C) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. D) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. E) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. i + Solve the initial-value problem = k × r with initial condition r(0) = i + 2j + 3k. Describe the solution curve. A) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. B) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. C) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. D) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. E) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. j + 3 k,a circle with centre (0, 0, 3) and radius Solve the initial-value problem = k × r with initial condition r(0) = i + 2j + 3k. Describe the solution curve. A) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. B) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. C) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. D) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. E) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. in the plane z = 3.
E) r(t) = Solve the initial-value problem = k × r with initial condition r(0) = i + 2j + 3k. Describe the solution curve. A) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. B) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. C) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. D) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. E) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. i + Solve the initial-value problem = k × r with initial condition r(0) = i + 2j + 3k. Describe the solution curve. A) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. B) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. C) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. D) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. E) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q55: Find the perimeter of the astroid

Q56: Find the radial and transverse components

Q57: A frictionless road turn is approximately circular

Q58: Suppose the position vector r(t) of an

Q59: Find the maximum and minimum values of

Q61: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Let : I

Q62: If r(t) , v(t) and a(t) are

Q63: A curve can have constant curvature <img

Q64: The mean distance from the Earth to

Q65: Find the curvature of the hyperbola xy