Multiple Choice
Find a polynomial f(x) of lowest possible degree such that the curve y = f(x) , 0 x 1, can be used to join the straight line segments y = 0, x 0, and y = 1, x 1, to form a curve along which a particle can travel at constant speed without experiencing discontinuous acceleration.
A) f(x) = 10  - 15
- 15 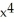 + 6
+ 6 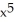
B) f(x) = 4 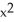 - 7
- 7 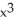 + 4
+ 4 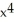
C) f(x) = 2  - 3
- 3 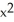 + 2
+ 2 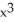
D) f(x) = 18 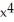 - 30
- 30 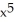 + 13
+ 13 
E) f(x) = 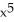 - 3
- 3  + 2
+ 2 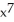
Correct Answer:

Verified
Correct Answer:
Verified
Q11: Solve the initial-value problem <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Solve
Q12: Show that the orbital speed of a
Q13: The period of the moon's orbit around
Q14: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Find and
Q15: What kind of curve is r(t) =
Q17: Find the point on the curve
Q18: Find an equation for the osculating circle
Q19: Which of the following parametrize the
Q20: If u and v are differentiable functions
Q21: A rocket with mass 60,000 kilogram (kg),