Multiple Choice
Find the cosine of the angle between the planes 3x + 3y - 6z = 12 and 7x - 5y + 2z = -8.
A) ± 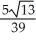
B) ± 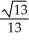
C) ± 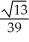
D) ± 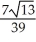
E) ± 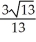
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q30: Describe the graph of 25x<sup>2</sup> - y<sup>2</sup>
Q31: Describe the surface with equation x<sup>2</sup> +
Q32: Find parametric equations of the straight line
Q33: Describe the set of points in 3-space
Q34: Find the equation of a plane that
Q36: Find the equation for the plane that
Q37: If u = 3i + j +
Q38: Let u and v be non-zero vectors
Q39: Which of the following is an equation
Q40: Describe the set of points in 3-space