Solved

Find an Equation of the Cylinder Generated by Lines Through

Question 56

Multiple Choice

Find an equation of the cylinder generated by lines through the curve y2 = x - y in the xy-plane that are parallel to the vector 2i + 2j + k.


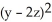A) Find an equation of the cylinder generated by lines through the curve y<sup>2</sup> = x - y in the xy-plane that are parallel to the vector 2i + 2j + k. A) = x - y B) = 2x - y C) = x - 2y D) = x - y E) = 2x - y = x - y
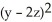B) Find an equation of the cylinder generated by lines through the curve y<sup>2</sup> = x - y in the xy-plane that are parallel to the vector 2i + 2j + k. A) = x - y B) = 2x - y C) = x - 2y D) = x - y E) = 2x - y = 2x - y
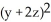C) Find an equation of the cylinder generated by lines through the curve y<sup>2</sup> = x - y in the xy-plane that are parallel to the vector 2i + 2j + k. A) = x - y B) = 2x - y C) = x - 2y D) = x - y E) = 2x - y = x - 2y
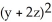D) Find an equation of the cylinder generated by lines through the curve y<sup>2</sup> = x - y in the xy-plane that are parallel to the vector 2i + 2j + k. A) = x - y B) = 2x - y C) = x - 2y D) = x - y E) = 2x - y = x - y
E) Find an equation of the cylinder generated by lines through the curve y<sup>2</sup> = x - y in the xy-plane that are parallel to the vector 2i + 2j + k. A) = x - y B) = 2x - y C) = x - 2y D) = x - y E) = 2x - y = 2x - y

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q51: Use Maple or other computer algebra software

Q52: Classify the symmetric matrix A = <img

Q53: Find all values of the real

Q54: Find a value c for which A

Q55: Find the area of a triangle that

Q57: Find the distance between the points (x,

Q58: Which of the following equations is an

Q59: Evaluate the determinant of the matrix <img

Q60: Use cylindrical coordinates [ r,

Q61: Describe the set of points in 3-space