Multiple Choice
Using the known geometric series representation 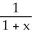 =
= 
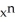 , valid for -1 < x < 1, find a power series representation for f(x) = ln(2 + x) in powers of x - 1. On what interval does the series converge to f(x) ?
, valid for -1 < x < 1, find a power series representation for f(x) = ln(2 + x) in powers of x - 1. On what interval does the series converge to f(x) ?
A) f(x) = ln 3 + 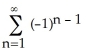

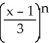 , for -0 < x 2
, for -0 < x 2
B) f(x) = ln 3 + 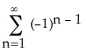

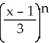 , for -2 < x 4
, for -2 < x 4
C) f(x) = ln 2 + 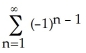

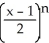 , for -1 < x 3
, for -1 < x 3
D) f(x) = ln 2 + 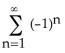

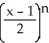 , for -1 < x < 3
, for -1 < x < 3
E) none of the above
Correct Answer:

Verified
Correct Answer:
Verified
Q30: If <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="If and
Q31: Which of the following descriptors apply
Q32: On what interval of values of x
Q33: How many nonzero terms of the known
Q34: Find the Taylor expansion of 4 <img
Q36: Find the first three nonzero terms in
Q37: Find the centre, radius, and interval
Q38: What is the largest positive constant K
Q39: If { <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="If {
Q40: For what values of x does