Multiple Choice
Find the Fourier series of the function f having period 2 and defined by f(x) = 0 if - < x 0 and f(x) = 1 if 0 < x .
A)  +
+ 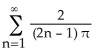 sin((2n - 1) x)
sin((2n - 1) x)
B) 1 + 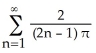 sin((2n - 1) x)
sin((2n - 1) x)
C)  +
+ 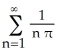 sin(2nx)
sin(2nx)
D) 1 + 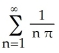 sin(2nx)
sin(2nx)
E)  +
+ 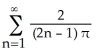 cos((2n - 1) x)
cos((2n - 1) x)
Correct Answer:

Verified
Correct Answer:
Verified
Q104: For what range of x can
Q105: Calculate the Maclaurin series for the
Q106: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt=" A)
Q107: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="
Q108: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Evaluate .
Q110: Which of the following descriptors apply
Q111: For what values of x does
Q112: If <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt=" If
Q113: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Let =
Q114: For what values of x does