Determine All Values of the Constant Real Number K So $\infty$

Multiple Choice

Determine all values of the constant real number k so that the Fourier series of the periodic function f(t) = 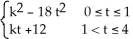, f(t + 4) = f(t)
Converges to f(t) for all t 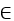(- $\infty$ , $\infty$ ) .

A) only -2
B) 6 and -5
C) - 2 and 6
D) only 6
E) -2 , -5 and 6