Solved

A Conic Section Is Given by the Equation 4x2 θ\theta To Find the New Equation of the Conic Section in 10xy

Question 70

Multiple Choice

A conic section is given by the equation 4x2 + 10xy + 4y2 = 36.Use rotation of coordinate axes through an appropriate acute angle θ\theta to find the new equation of the conic section in the uv-coordinate axes , where x = u cos( θ\theta ) - v sin( θ\theta ) , y = u sin( θ\theta ) + v cos( θ\theta ) . Then identify the conic section.


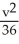A) A conic section is given by the equation 4x<sup>2</sup> + 10xy + 4y<sup>2</sup> = 36.Use rotation of coordinate axes through an appropriate acute angle \theta to find the new equation of the conic section in the uv-coordinate axes , where x = u cos( \theta ) - v sin( \theta ) , y = u sin( \theta ) + v cos( \theta ) . Then identify the conic section. 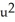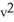A) + = 1, an ellipse B) + = 4, a circle C) - = 1, a hyperbola D) + = 1, an ellipse E) - = 1, a hyperbola + A conic section is given by the equation 4x<sup>2</sup> + 10xy + 4y<sup>2</sup> = 36.Use rotation of coordinate axes through an appropriate acute angle \theta to find the new equation of the conic section in the uv-coordinate axes , where x = u cos( \theta ) - v sin( \theta ) , y = u sin( \theta ) + v cos( \theta ) . Then identify the conic section. A) + = 1, an ellipse B) + = 4, a circle C) - = 1, a hyperbola D) + = 1, an ellipse E) - = 1, a hyperbola = 1, an ellipse
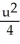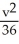B) A conic section is given by the equation 4x<sup>2</sup> + 10xy + 4y<sup>2</sup> = 36.Use rotation of coordinate axes through an appropriate acute angle \theta to find the new equation of the conic section in the uv-coordinate axes , where x = u cos( \theta ) - v sin( \theta ) , y = u sin( \theta ) + v cos( \theta ) . Then identify the conic section. 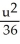A) + = 1, an ellipse B) + = 4, a circle C) - = 1, a hyperbola D) + = 1, an ellipse E) - = 1, a hyperbola + A conic section is given by the equation 4x<sup>2</sup> + 10xy + 4y<sup>2</sup> = 36.Use rotation of coordinate axes through an appropriate acute angle \theta to find the new equation of the conic section in the uv-coordinate axes , where x = u cos( \theta ) - v sin( \theta ) , y = u sin( \theta ) + v cos( \theta ) . Then identify the conic section. A) + = 1, an ellipse B) + = 4, a circle C) - = 1, a hyperbola D) + = 1, an ellipse E) - = 1, a hyperbola = 4, a circle
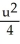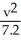C) A conic section is given by the equation 4x<sup>2</sup> + 10xy + 4y<sup>2</sup> = 36.Use rotation of coordinate axes through an appropriate acute angle \theta to find the new equation of the conic section in the uv-coordinate axes , where x = u cos( \theta ) - v sin( \theta ) , y = u sin( \theta ) + v cos( \theta ) . Then identify the conic section. A) + = 1, an ellipse B) + = 4, a circle C) - = 1, a hyperbola D) + = 1, an ellipse E) - = 1, a hyperbola - A conic section is given by the equation 4x<sup>2</sup> + 10xy + 4y<sup>2</sup> = 36.Use rotation of coordinate axes through an appropriate acute angle \theta to find the new equation of the conic section in the uv-coordinate axes , where x = u cos( \theta ) - v sin( \theta ) , y = u sin( \theta ) + v cos( \theta ) . Then identify the conic section. A) + = 1, an ellipse B) + = 4, a circle C) - = 1, a hyperbola D) + = 1, an ellipse E) - = 1, a hyperbola = 1, a hyperbola
D) A conic section is given by the equation 4x<sup>2</sup> + 10xy + 4y<sup>2</sup> = 36.Use rotation of coordinate axes through an appropriate acute angle \theta to find the new equation of the conic section in the uv-coordinate axes , where x = u cos( \theta ) - v sin( \theta ) , y = u sin( \theta ) + v cos( \theta ) . Then identify the conic section. A) + = 1, an ellipse B) + = 4, a circle C) - = 1, a hyperbola D) + = 1, an ellipse E) - = 1, a hyperbola + A conic section is given by the equation 4x<sup>2</sup> + 10xy + 4y<sup>2</sup> = 36.Use rotation of coordinate axes through an appropriate acute angle \theta to find the new equation of the conic section in the uv-coordinate axes , where x = u cos( \theta ) - v sin( \theta ) , y = u sin( \theta ) + v cos( \theta ) . Then identify the conic section. A) + = 1, an ellipse B) + = 4, a circle C) - = 1, a hyperbola D) + = 1, an ellipse E) - = 1, a hyperbola = 1, an ellipse
E) A conic section is given by the equation 4x<sup>2</sup> + 10xy + 4y<sup>2</sup> = 36.Use rotation of coordinate axes through an appropriate acute angle \theta to find the new equation of the conic section in the uv-coordinate axes , where x = u cos( \theta ) - v sin( \theta ) , y = u sin( \theta ) + v cos( \theta ) . Then identify the conic section. A) + = 1, an ellipse B) + = 4, a circle C) - = 1, a hyperbola D) + = 1, an ellipse E) - = 1, a hyperbola - A conic section is given by the equation 4x<sup>2</sup> + 10xy + 4y<sup>2</sup> = 36.Use rotation of coordinate axes through an appropriate acute angle \theta to find the new equation of the conic section in the uv-coordinate axes , where x = u cos( \theta ) - v sin( \theta ) , y = u sin( \theta ) + v cos( \theta ) . Then identify the conic section. A) + = 1, an ellipse B) + = 4, a circle C) - = 1, a hyperbola D) + = 1, an ellipse E) - = 1, a hyperbola = 1, a hyperbola

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q65: The equation of a conic section in

Q66: Convert the point with Cartesian coordinates (-1,

Q67: Find the equation of the parabola whose

Q68: The equations x(t) = <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg"

Q69: Find the area bounded by the

Q71: If x = f( <span class="ql-formula"

Q72: Express <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt=" Express

Q73: Transform the polar equation r =

Q74: Find the arc length of r

Q75: Find an equation of a parabola