Multiple Choice
A plane curve C is given parametrically by x = tan(t) - 2, y = sec(t) , t 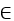 (-
(- 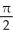 ,
, 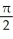 ) .Find the Cartesian equation of the curve C.
) .Find the Cartesian equation of the curve C.
A) 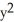 -
- 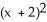 = 1, y 1
= 1, y 1
B) 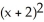 -
- 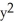 = 1, y 1
= 1, y 1
C) 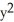 +
+ 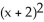 = 1, - < y <
= 1, - < y <
D) 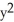 -
- 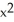 = 5, -1 y 1
= 5, -1 y 1
E) 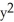 -
- 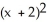 = 1, y - 1
= 1, y - 1
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q26: Find the points of intersection of
Q27: Find the equation to the ellipse for
Q28: Determine the points where the parametric curve
Q29: Find the equation of the tangent line
Q30: Show that the total arc length
Q32: Find the length of one arch
Q33: Find the area bounded by one
Q34: Find the slope of the curve x
Q35: Find the length of the curve x
Q36: Find the equation of the tangent line