Multiple Choice
Find 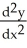 at the highest point on the cycloid x = a
at the highest point on the cycloid x = a
- a sin
, y = a - a cos
.
A) - 
B) - 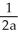
C) 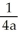
D) 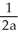
E) 
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q1: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt=" " class="answers-bank-image d-block"
Q3: Determine the area above the x-axis
Q4: Find a rectangular equation equivalent to
Q5: Find parametric equations of the plane
Q6: Find the arc length of r
Q7: Find the length of x =
Q8: Where does the curve x = 2
Q9: Parametrize the curve y = <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg"
Q10: Find a rectangular equation equivalent to
Q11: Find the slope of the curve x