Solved

Find the Cartesian Equation of the Straight Line Tangent to the Plane

Question 112

Multiple Choice

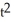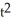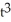Find the Cartesian equation of the straight line tangent to the plane curve given parametrically by the equations x(t) = Find the Cartesian equation of the straight line tangent to the plane curve given parametrically by the equations x(t) = + 2t + 2, y(t) = 1 - 3 - 2 at the point on the curve where t = -1. A) x -3y -1 = 0 B) y =1 C) y = x + 1 D) 3x -y -3 = 0 E) y = 3x -7 + 2t + 2, y(t) = 1 - 3 Find the Cartesian equation of the straight line tangent to the plane curve given parametrically by the equations x(t) = + 2t + 2, y(t) = 1 - 3 - 2 at the point on the curve where t = -1. A) x -3y -1 = 0 B) y =1 C) y = x + 1 D) 3x -y -3 = 0 E) y = 3x -7 - 2 Find the Cartesian equation of the straight line tangent to the plane curve given parametrically by the equations x(t) = + 2t + 2, y(t) = 1 - 3 - 2 at the point on the curve where t = -1. A) x -3y -1 = 0 B) y =1 C) y = x + 1 D) 3x -y -3 = 0 E) y = 3x -7 at the point on the curve where t = -1.


A) x -3y -1 = 0
B) y =1
C) y = x + 1
D) 3x -y -3 = 0
E) y = 3x -7

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q104: Find the area bounded by the

Q105: Find the area bounded by the

Q106: Find the equation of the parabola passing

Q107: Find the area of the surface generated

Q108: If the equation f( <span

Q109: Find the area of the surface

Q110: Find the area of the surface

Q111: The maximum distance of the Earth from

Q113: Find the centre, eccentricity, and foci of

Q114: Which of the following plane parametric