Multiple Choice
Find the length of the curve x = 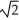 t, y =
t, y = 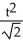 , 0 t 1.
, 0 t 1.
A) 1 + 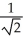 ln(
ln( 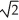 + 1) units
+ 1) units
B) 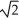 +
+ 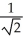 ln(
ln( 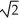 + 1) units
+ 1) units
C) 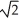 -
- 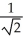 ln(
ln( 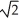 + 1) units
+ 1) units
D) 1 - 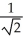 ln(
ln( 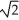 + 1) units
+ 1) units
E) 1 + 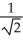 ln(
ln( 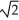 ) units
) units
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q7: Find the length of x =
Q8: Where does the curve x = 2
Q9: Parametrize the curve y = <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg"
Q10: Find a rectangular equation equivalent to
Q11: Find the slope of the curve x
Q13: Sketch the polar curve r<sup>2</sup> = 9
Q14: Convert x<sup>2</sup> + y<sup>2</sup> = xy to
Q15: Find the area of the surface
Q16: A plane curve C is given parametrically
Q17: Find an equation of a parabola satisfying