Multiple Choice
For what real values of the constant k does the region lying under the curve y = 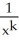 above the x-axis and to the right of the line x = 1 have infinite area but gives rise to a solid with finite volume when rotated about the x-axis?
above the x-axis and to the right of the line x = 1 have infinite area but gives rise to a solid with finite volume when rotated about the x-axis?
A)  < k 1
< k 1
B)  < k < 1
< k < 1
C)  < k <
< k <
D) 0 < k < 
E) 0 < k 1
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q104: Find the centroid of the region bounded
Q105: A supplier of cell phones realizes a
Q106: Find the solution of the initial-value problem
Q107: A conical reservoir (vertex down) having
Q108: The equations x = -1, x =
Q110: Find the volume of the solid
Q111: Find the centre of mass of a
Q112: If R is the region enclosed
Q113: Find the volume of the solid obtained
Q114: A force of f pounds acting along