Let R Be the Plane Region Enclosed by the Graphs $\pi$

Multiple Choice

Let R be the plane region enclosed by the graphs of y = f(x) and y = g(x) from x = a to x = b , where a > 0(as shown in the figure below) .If the solid generated by revolving the plane region R about the x-axis has the same volume as the solid generated by revolving the region R about the y-axis , then f and g satisfy which equation for all x > 0?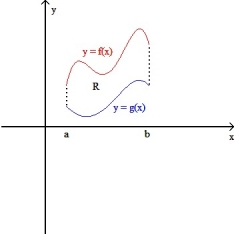

A) f(x) = - g(x)
B) f(x) + g(x) = x
C) f(x) + g(x) =
D) f(x) + g(x) = 2x
E) f(x) + g(x) = $\pi$ (x -2)