Multiple Choice
A ball of radius r has volume V(r) = 
 cubic units. This volume can be regarded as a sum of volumes of concentric spherical shells having radii x units (where 0 x r) and thickness dx. Use this fact to find the surface area S(r) of a sphere of radius r.
cubic units. This volume can be regarded as a sum of volumes of concentric spherical shells having radii x units (where 0 x r) and thickness dx. Use this fact to find the surface area S(r) of a sphere of radius r.
A) S(r) = 4 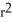 square units
square units
B) S(r) = 8 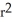 square units
square units
C) S(r) = 2  square units
square units
D) S(r) = 8 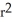 square units
square units
E) S(r) = 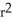 square units
square units
Correct Answer:

Verified
Correct Answer:
Verified
Q13: Find the length of the curve y
Q14: Determine a multiplier (integrating factor) of the
Q15: Find the solution of the initial-value problem
Q16: Find the area of the surface
Q17: A finite region R is contained in
Q19: Find the area of the surface generated
Q20: Solve the initial-value problem <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Solve
Q21: Determine the centroid of the finite plane
Q22: Find the area of the surface
Q23: What is the present value of a