Solved

Find the Centroid of the Finite Plane Region Bounded by the Curve

Question 97

Multiple Choice

Find the centroid of the finite plane region bounded by the curve y = 4 - x2 and the liney = x + 2.


A) Find the centroid of the finite plane region bounded by the curve y = 4 - x<sup>2</sup> and the liney = x + 2. A) B) C) D) E)
B) Find the centroid of the finite plane region bounded by the curve y = 4 - x<sup>2</sup> and the liney = x + 2. A) B) C) D) E)
C) Find the centroid of the finite plane region bounded by the curve y = 4 - x<sup>2</sup> and the liney = x + 2. A) B) C) D) E)
D) Find the centroid of the finite plane region bounded by the curve y = 4 - x<sup>2</sup> and the liney = x + 2. A) B) C) D) E)
E) Find the centroid of the finite plane region bounded by the curve y = 4 - x<sup>2</sup> and the liney = x + 2. A) 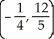B) 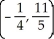C) 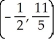D) 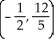E)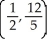

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q92: If a school bus is travelling 90

Q93: Find the volume of a solid

Q94: Find the volume of the solid

Q95: A normal distribution has a mean of

Q96: Solve the initial-value problem <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Solve

Q98: Find the area of the surface

Q99: Find the volume of the solid

Q100: Find the moment about the line x

Q101: Find the value of the constant real

Q102: The plane region defined by 0 ≤