A Tank Contains 200 Litres of Fluid in Which 60 $~~~~~~~~$

Multiple Choice

A tank contains 200 litres of fluid in which 60 grams of salt is dissolved. A brine solution of 2 grams of salt per litre is pumped into the tank at a rate of 2 litres/minute. The well-stirred solution is then pumped out at the same rate.(a) Write the differential equation in terms of Q(t) and t and write the initial condition to model this problem. (Q(t) should represent the amount of salt in the tank at time t) .(b) Solve the equation in part (a) .(c) How much salt will be present in the tank after a long period of time?

A) (a) 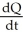= 2 - 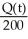, Q(0) = 60 $~~~~~~~~$ (b) Q(t) = 200 - 340 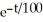$~~~~~~~~$ (c) 200 grams
B) (a) 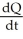= 4 - 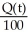, Q(0) = 60 $~~~~~~~~$ (b) Q(t) = 400 - 340 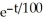$~~~~~~~~$ (c) 400 grams
C) (a) 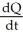= 400 - 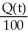, Q(0) = 60 $~~~~~~~~$ (b) Q(t) = 40 - 34 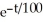$~~~~~~~~$ (c) 40 grams
D) (a) 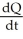= 400 - 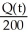, Q(0) = 60 $~~~~~~~~$ (b) Q(t) = 4 - 3.4 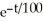$~~~~~~~~$ (c) 4 grams
E) (a) 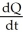= 400 - Q(t) , Q(0) = 60 $~~~~~~~~$ (b) Q(t) = 400 - 340 $~~~~~~~~$ (c) 400 grams