Solved

Find an Upper Bound for the Size of the Error

Question 84

Multiple Choice

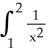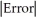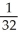Find an upper bound for the size of the error if the Trapezoidal Rule using 4 equal subintervals is used to approximate the integral Find an upper bound for the size of the error if the Trapezoidal Rule using 4 equal subintervals is used to approximate the integral dx. Is the error positive or negative? A) < , Error < 0 B) < , Error > 0 C) < , Error > 0 D) < , Error < 0 E) < , Error < 0 dx. Is the error positive or negative?


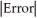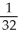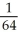A) Find an upper bound for the size of the error if the Trapezoidal Rule using 4 equal subintervals is used to approximate the integral dx. Is the error positive or negative? A) < , Error < 0 B) < , Error > 0 C) < , Error > 0 D) < , Error < 0 E) < , Error < 0 < Find an upper bound for the size of the error if the Trapezoidal Rule using 4 equal subintervals is used to approximate the integral dx. Is the error positive or negative? A) < , Error < 0 B) < , Error > 0 C) < , Error > 0 D) < , Error < 0 E) < , Error < 0 , Error < 0
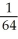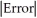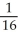B) Find an upper bound for the size of the error if the Trapezoidal Rule using 4 equal subintervals is used to approximate the integral dx. Is the error positive or negative? A) < , Error < 0 B) < , Error > 0 C) < , Error > 0 D) < , Error < 0 E) < , Error < 0 < Find an upper bound for the size of the error if the Trapezoidal Rule using 4 equal subintervals is used to approximate the integral dx. Is the error positive or negative? A) < , Error < 0 B) < , Error > 0 C) < , Error > 0 D) < , Error < 0 E) < , Error < 0 , Error > 0
C) Find an upper bound for the size of the error if the Trapezoidal Rule using 4 equal subintervals is used to approximate the integral dx. Is the error positive or negative? A) < , Error < 0 B) < , Error > 0 C) < , Error > 0 D) < , Error < 0 E) < , Error < 0 < Find an upper bound for the size of the error if the Trapezoidal Rule using 4 equal subintervals is used to approximate the integral dx. Is the error positive or negative? A) < , Error < 0 B) < , Error > 0 C) < , Error > 0 D) < , Error < 0 E) < , Error < 0 , Error > 0
D) Find an upper bound for the size of the error if the Trapezoidal Rule using 4 equal subintervals is used to approximate the integral dx. Is the error positive or negative? A) < , Error < 0 B) < , Error > 0 C) < , Error > 0 D) < , Error < 0 E) < , Error < 0 < Find an upper bound for the size of the error if the Trapezoidal Rule using 4 equal subintervals is used to approximate the integral dx. Is the error positive or negative? A) < , Error < 0 B) < , Error > 0 C) < , Error > 0 D) < , Error < 0 E) < , Error < 0 , Error < 0
E) Find an upper bound for the size of the error if the Trapezoidal Rule using 4 equal subintervals is used to approximate the integral dx. Is the error positive or negative? A) < , Error < 0 B) < , Error > 0 C) < , Error > 0 D) < , Error < 0 E) < , Error < 0 < Find an upper bound for the size of the error if the Trapezoidal Rule using 4 equal subintervals is used to approximate the integral dx. Is the error positive or negative? A) < , Error < 0 B) < , Error > 0 C) < , Error > 0 D) < , Error < 0 E) < , Error < 0 , Error < 0

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q79: Evaluate the improper integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg"

Q80: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt=" Evaluate

Q81: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Evaluate dx.

Q82: Let G(x) = <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="

Q83: For what values of the constant

Q85: The integral I = <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="The

Q86: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt=" Evaluate

Q87: Find the Midpoint Rule approximation <img

Q88: The values of a continuous function f

Q89: Integrate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Integrate A)