Use Simpson's Rule with 4 and 8 Subintervals to Approximate $\approx$

Multiple Choice

Use Simpson's Rule with 4 and 8 subintervals to approximate I = 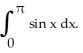Give your answers to 5 decimal places. What are the actual errors in these approximations?

A) S₄ $\approx$ 2.00466, S₈ $\approx$ 2.00029, I - S₄ $\approx$ -0.00466, I - S₈ $\approx$ -0.00029
B) S₄ $\approx$ 2.00456, S₈ $\approx$ 2.00027, I - S₄ $\approx$ -0.00456, I - S₈ $\approx$ -0.00027
C) S₄ $\approx$ 2.00446, S₈ $\approx$ 2.00024, I - S₄ $\approx$ -0.00446, I - S₈ $\approx$ -0.00024
D) S₄ $\approx$ 2.00436, S₈ $\approx$ 2.00020, I - S₄ $\approx$ -0.00436, I - S₈ $\approx$ -0.00020
E) S₄ $\approx$ 2.00476, S₈ $\approx$ 2.00031, I - S₄ $\approx$ -0.00476, I - S₈ $\approx$ -0.00031