By Interpreting It as the Area of a Region in the Xy-Plane

Multiple Choice

By interpreting it as the area of a region in the xy-plane, evaluate the limit .

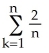
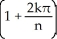
A) 2 + 2 $\pi$ (the area of the trapezoidal region under y = 1 + $\pi$ x, above y = 0 from x = 0 to x = 2)
B) 1 + $\pi$ (the area of the trapezoidal region under y = 1 + 2 $\pi$ x, above y = 0 from x = 0 to x = 1)
C) 2 + 4 $\pi$ (the area of the trapezoidal region under y = 1 + 2 $\pi$ x, above y = 0 from x = 0 to x = 2)
D) 4 + 2 $\pi$ (the area of the trapezoidal region under y = 2 + $\pi$ x, above y = 0 from x = 0 to x = 2)
E) 2 + 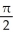(the area of the trapezoidal region under y = 2 + $\pi$ x, above y = 0 from x = 0 to x = 1)