Solved

Let J = Dx

Question 57

Multiple Choice

Let J = Let J = dx. The substitution u = tan(3x) transforms the integral J into : A) B) C) D) E) dx. The substitution u = tan(3x) transforms the integral J into :


A) Let J = dx. The substitution u = tan(3x) transforms the integral J into : A) B) C) D) E)
B) Let J = dx. The substitution u = tan(3x) transforms the integral J into : A) B) C) D) E)
C) Let J = dx. The substitution u = tan(3x) transforms the integral J into : A) B) C) D) E)
D) Let J = dx. The substitution u = tan(3x) transforms the integral J into : A) B) C) D) E)
E) Let J = 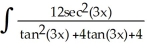dx. The substitution u = tan(3x) transforms the integral J into : A) 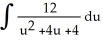B) 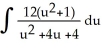C) 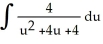D) 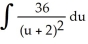E)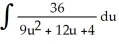

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q52: Find the inflection point of the function

Q53: Evaluate the definite integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Evaluate

Q54: Write the following limit as a definite

Q55: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Evaluate dx.

Q56: Evaluate the integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Evaluate the

Q58: By interpreting it as the area

Q59: The limit <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt=" The

Q60: Write the area under the curve

Q61: Calculate the lower Riemann sum for f(x)

Q62: Find the point on the graph of