Solved

Give the Iteration Formula for Finding the Roots of the Equation

Question 67

Multiple Choice

Give the iteration formula for finding the roots of the equation sin x - x2 = 0 using Newton's Method.


A) Give the iteration formula for finding the roots of the equation sin x - x<sup>2</sup> = 0 using Newton's Method. A) = - B) = - C) = + D) = - E) = + = Give the iteration formula for finding the roots of the equation sin x - x<sup>2</sup> = 0 using Newton's Method. A) = - B) = - C) = + D) = - E) = + - Give the iteration formula for finding the roots of the equation sin x - x<sup>2</sup> = 0 using Newton's Method. A) = - B) = - C) = + D) = - E) = +
B) Give the iteration formula for finding the roots of the equation sin x - x<sup>2</sup> = 0 using Newton's Method. A) = - B) = - C) = + D) = - E) = + = Give the iteration formula for finding the roots of the equation sin x - x<sup>2</sup> = 0 using Newton's Method. A) = - B) = - C) = + D) = - E) = + - Give the iteration formula for finding the roots of the equation sin x - x<sup>2</sup> = 0 using Newton's Method. A) = - B) = - C) = + D) = - E) = +
C) Give the iteration formula for finding the roots of the equation sin x - x<sup>2</sup> = 0 using Newton's Method. A) = - B) = - C) = + D) = - E) = + = Give the iteration formula for finding the roots of the equation sin x - x<sup>2</sup> = 0 using Newton's Method. A) = - B) = - C) = + D) = - E) = + + Give the iteration formula for finding the roots of the equation sin x - x<sup>2</sup> = 0 using Newton's Method. A) = - B) = - C) = + D) = - E) = +
D) Give the iteration formula for finding the roots of the equation sin x - x<sup>2</sup> = 0 using Newton's Method. A) = - B) = - C) = + D) = - E) = + = Give the iteration formula for finding the roots of the equation sin x - x<sup>2</sup> = 0 using Newton's Method. A) = - B) = - C) = + D) = - E) = + - Give the iteration formula for finding the roots of the equation sin x - x<sup>2</sup> = 0 using Newton's Method. A) = - B) = - C) = + D) = - E) = +
E) Give the iteration formula for finding the roots of the equation sin x - x<sup>2</sup> = 0 using Newton's Method. A) = - B) = - C) = + D) = - E) = + = Give the iteration formula for finding the roots of the equation sin x - x<sup>2</sup> = 0 using Newton's Method. A) = - B) = - C) = + D) = - E) = + + Give the iteration formula for finding the roots of the equation sin x - x<sup>2</sup> = 0 using Newton's Method. 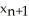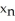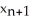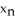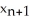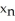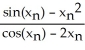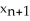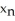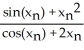A) = - B) = - C) = + D) = - E) = +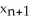

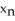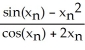
Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q62: Find the height of the circular cylinder

Q63: Evaluate the limit . <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Evaluate

Q64: Find all inflection points of the graph

Q65: Find all local extreme values of the

Q66: Compute the Maclaurin polynomial of degree 3

Q68: Evaluate the limit . <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg"

Q69: Find the roots of the equation ln

Q70: Find the inflection points of the graph

Q71: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt=" A)

Q72: Given that <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Given that