Solved

Suppose Newton's Method Applied to F(x) = Is Used ≠\neq

Question 77

Essay

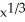Suppose Newton's Method applied to f(x) = Suppose Newton's Method applied to f(x) = is used to find the root of the equation = 0 with initial guess x<sub>0</sub> = r \neq 0. What result does the first iteration of the method yield? The second iteration? The nth iteration? Why do these not converge to the obvious root x = 0 no matter how close the initial guess r was to that root? is used to "find"the root of the equation Suppose Newton's Method applied to f(x) = is used to find the root of the equation = 0 with initial guess x<sub>0</sub> = r \neq 0. What result does the first iteration of the method yield? The second iteration? The nth iteration? Why do these not converge to the obvious root x = 0 no matter how close the initial guess r was to that root? = 0 with initial guess x0 = r ≠\neq 0. What result does the first iteration of the method yield? The second iteration? The nth iteration? Why do these not converge to the obvious root x = 0 no matter how close the initial guess r was to that root?

Correct Answer:

verifed

Verified

x1 = -2r, x2 = 4r, ..., xn = blured image r.

View Answer

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q72: Given that <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Given that

Q73: An aircraft is climbing at a 30-degree

Q74: The height of a right circular

Q75: Find the equations of the vertical asymptotes

Q76: Evaluate . <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Evaluate .

Q78: A plane is flying horizontally at an

Q79: If f(x) is a polynomial of degree

Q80: Use the table of values below to

Q81: Given f(x) = <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Given f(x)

Q82: Find all local extreme values of the