Multiple Choice
Find and classify all the local extrema of the function f(x) = x - sin2x.
A) local minima at x = k + 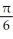 and local maxima at x = k -
and local maxima at x = k - 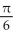 , where k is an integer
, where k is an integer
B) local maxima at x = k + 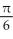 and local minima at x = k -
and local minima at x = k - 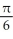 , where k is an integer
, where k is an integer
C) local maxima at x = k + 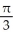 and local minima at x = k -
and local minima at x = k -  , where k is an integer
, where k is an integer
D) local minima at x = k + 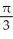 and local maxima at x = k -
and local maxima at x = k - 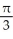 , where k is an integer
, where k is an integer
E) local minima at x = 2k + 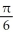 and local maxima at x = 2k -
and local maxima at x = 2k - 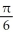 , where k is an integer
, where k is an integer
Correct Answer:

Verified
Correct Answer:
Verified
Q38: Use Newton's Method to find the roots
Q39: The power P (watts) in an electric
Q40: Find the minimum values of the function
Q41: Use information from the function and its
Q42: Find the absolute maximum and absolute
Q44: A girl is on the bank of
Q45: Newton's Method with the initial approximation x<sub>1</sub>
Q46: The function f(x) = 3x<sup>5</sup> + Ax<sup>4</sup>
Q47: The graph of f(x) = 3 <img
Q48: Evaluate the limit . <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg"