Solved

Let G Be a Polynomial Function Such That (X)

Question 120

Multiple Choice

Let g be a polynomial function such that 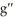Let g be a polynomial function such that (x) = (x + 2) ( - 10x -24) . Find the x-coordinate of all inflection points of the graph of g. A) only -2 B) -2 and 12 C) - 2 , 4, and 6 D) only 12 E) -2, - 4, and -6 (x) = (x + 2) ( Let g be a polynomial function such that (x) = (x + 2) ( - 10x -24) . Find the x-coordinate of all inflection points of the graph of g. A) only -2 B) -2 and 12 C) - 2 , 4, and 6 D) only 12 E) -2, - 4, and -6 - 10x -24) . Find the x-coordinate of all inflection points of the graph of g.


A) only -2
B) -2 and 12
C) - 2 , 4, and 6
D) only 12
E) -2, - 4, and -6

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q115: Find the Taylor polynomial of degree 4

Q116: Find a linear approximation suitable for estimating

Q117: Find the largest possible volume of

Q118: Evaluate the limit . <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Evaluate

Q119: A boat is pulled toward a dock

Q121: Use Newton's Method to find the solution

Q122: Find the extreme values of f(x) =

Q123: Find a suitable linear approximation that lets

Q124: Find the equations of all horizontal asymptotes

Q125: Evaluate the limit . <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9661/.jpg" alt="Evaluate